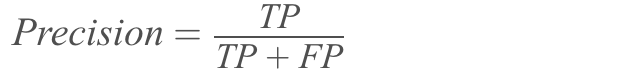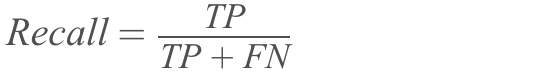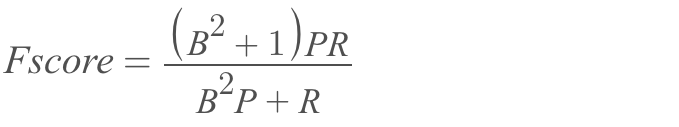What is F-score in Python?

In this shot, we will be discussing F-score in Python.

Introduction

Machine learning algorithms are evolving every day. Several algorithms are designed and developed to predict an outcome to a problem or classify data. Some work very well by predicting a value with a slight error to the correct value, while others are not as accurate. Several scores are designed to check whether an algorithm has performed well or not.

Precision is a score that tells us what ratio of the positives identified by our algorithm was actually correct.

  • TPTP: True positive; the positives identified by your algorithm are actually positives.
  • FPFP: False positive; the positives identified by your algorithm that are actually negatives.

Recall is a score that tells us what ratio of actual positives was identified as positive by our algorithm.

  • FNFN: False negatives; the negatives identified by your algorithm that are actually positives.

The scores mentioned above are good metrics to measure the performance of algorithms. However, they fail in certain cases.

The F-score is the weighted harmonic mean of Precision and Recall. This means that this score is only high when both Precision and Recall are high, and low when either is low. The F-score helps the user get the true score of how well their algorithm is performing.

  • BB = Weight that defines the importance of Precision and Recall
  • PP = Precision
  • RR = Recall
def f1(matrix):
    
    tp=int(matrix[0,0]) #1st cell of the matrix is true positive
    fp=int(matrix[0,1])#1st row second cell of the matrix is false positive
    fn=int(matrix[1,0])#2nd row 1st cell is false negative
    tn=int(matrix[1,1])#2nd row 2nd cell if true negative
    precision=tp/(tp+fp)
    print("Precision: ",precision)
    recall=tp/(tp+fn)
    print("Recall: ",recall)
    f1=2*(precision*recall)/(precision+recall)
    return f1
def confusion_matrix(pred,original):
    #0 is considered negative and 1 is considered positive.
    matrix=np.zeros((2,2))
    for i in range(len(pred)):
        if int(pred[i])==1 and int(original[i])==1:
            matrix[0,0]+=1
        elif int(pred[i])==1 and int(original[i])==0:
            matrix[0,1]+=1
        elif int(pred[i])==0 and int(original[i])==1:
            matrix[1,0]+=1
        elif int(pred[i])==0 and int(original[i])==0:
            matrix[1,1]+=1
    return matrix

The code above is to calculate the F-score, where the value of BB is set to 1. This code is for a confusion matrix of dimensions 2x2. A confusion matrix stores the summary of the results.

Free Resources

License: Creative Commons-Attribution-ShareAlike 4.0 (CC-BY-SA 4.0)