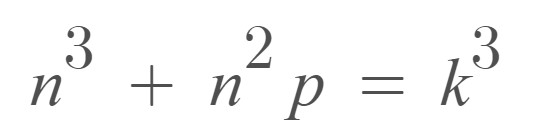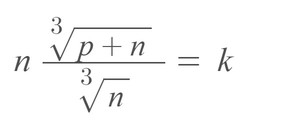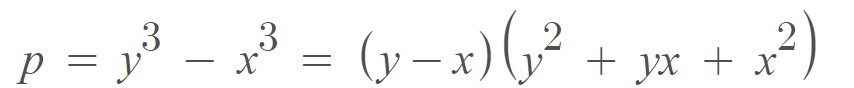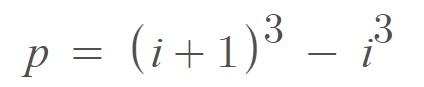#    
## Problem statement

The Project Euler prime cube partnership problem states:

"_There are some prime values, p, for which there exists a positive integer, n, such that the expression $n^3 + n^2 * p$ is a perfect cube._


_For example, when $p = 19, 8^3 + 8^2 * 19 = 12^3.$_

_What is perhaps most surprising is that for each prime with this property, the value of n is unique, and there are only four such primes below one-hundred._

_How many primes below one million have this remarkable property?_"

#key# Problem source: https://gfredericks.com/things/project_euler/131 #key#

#    
## Solution
To solve this problem, let's start with the following equation: 
![](/api/edpresso/shot/4784315791048704/image/6652529793826816)

In the equation above, $k$ is the *perfect prime* and $p$ is *prime*.

Now, let's simplify this equation: 

![](/api/edpresso/shot/4784315791048704/image/6167166277124096)
![](/api/edpresso/shot/4784315791048704/image/5033888287555584)

![](/api/edpresso/shot/4784315791048704/image/6089531119370240)

![](/api/edpresso/shot/4784315791048704/image/5004453626773504)

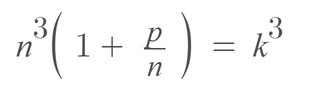
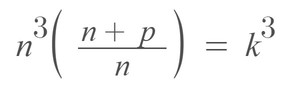
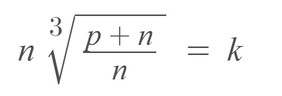
From the calculation above, we can conclude that if $k$ is an integer, then $n$ and $n + p$ must be perfect cubes because both terms are under the cube root formula. 

Now, if both $n$ and $n+p$ are perfect cubes, then we can replace both of them with new terms, as shown below: 

* $n = x^3$
* $p + n = y^3$

Both $x$ and $y$ belong to the integer set. 

Also,

* $p + n = y^3$ 
* $p = y^3 - n$ 
* $p = y^3 - x^3$ 
So $p$ is the difference between 2 cubes.

The difference between cube formulas can also be written as follows: 

![](/api/edpresso/shot/4784315791048704/image/5065543563870208)

From the equation above, we can see that the term $y-x$ is a factor of $p$, which means $p$ is divisible by $y-x$. However, if we want $p$ to be prime, then $y-x$ must be equal to 1.

$y - x = 1$   
 
This indicates that $x$ and $y$ are *two consecutive numbers* because their difference is 1.     

We can rewrite the equation above as follows:    
![](/api/edpresso/shot/4784315791048704/image/4640092198535168)


Now, we only need to check the following equation for which value of $p$ is below one million (1000000).     
For $i = 577$, we get $p = 578 ^3 - 577 ^3  = 100519$, which is greater than 1 million.    


#   
## Code

To write the code, we only need to check the values up to 577 because values greater than 577 do not satisfy the equation.   
     
We can find the solution with the following code:



#include <iostream>
using namespace std;

bool isprime(int number) {
 bool ans = true;
 if (number == 0 || number == 1) {
 ans = false;
 }
 else {
 for (int i = 2; i <= number / 2; ++i) {
 if (number % i == 0) {
 ans = false;
 break;
 }
 }
 }
 return ans;
}

int main() {
 int res = 0;
 for (int i = 1; i < 577; i++) {
 int cube1 = (i + 1) * (i + 1) * (i + 1);
 int cube2 = i * i * i;
 if (isprime( cube1 - cube2))
 res++;
 }
 cout << res << endl;

 return 0;
}

The code above gives the answer $173$ as the number of primes with this property.

Project Euler: Prime cube partnership

There are 173 primes under one million where $ n^3 + n^2 \cdot p $ is a perfect cube with a unique n.