How to find num of positive integral solutions for x1+x2+...+xk=n

Overview

In this Answer, we'll learn how to find the number of positive integral solutions for the equation of form x1 + x2 + ... + xk = n.

Solution

This problem is equivalent to finding the number of ways to distribute nn identical objects to kk partitions such that each partition has at least one object.

If ithith partition contains xixi objects, then if we take the sum of sizes of all kk partitions, we obtain the identical equation: x1 + x2 + ... + xk = n.

Let's consider a similar example to understand how to solve this combinatorial problem:

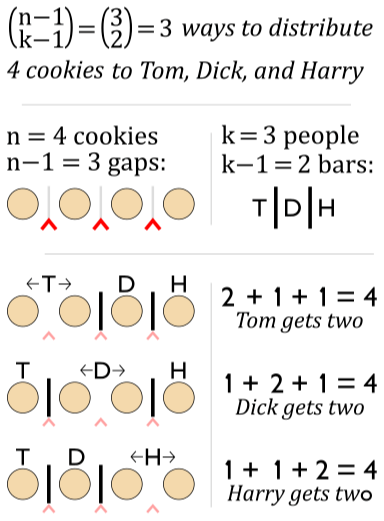
“Colored circle starsbars 1”, by Guy vandegrift , licensed under CC BY-SA 4.0
“Colored circle starsbars 1”, by Guy vandegrift , licensed under CC BY-SA 4.0

We want to distribute 4 cookies to 3 people such that each person gets at least 1 cookie. Each cookie is represented by a colored circle. 4 circles need 3 gaps which are represented by a red caret. Since there are 3 people, we need 2 bars (|) to fill any of the 3 gaps. This problem is now reduced to finding the binomial coefficient:C (n−1k−1)=(n−1)!(k−1)!(n−k)! \binom{n-1}{k-1} = \frac{(n-1)!}{ (k-1)!( n-k)!}

In C++ implementation, we use m! = m * (m - 1)! to calculate factorials. We store factorials in unsigned long long type, so we cannot compute values larger than 20!.

Code example

Let's look at the code below:

#include <iostream>
using namespace std;
//calculates n!, max value of n = 20
unsigned long long factorial(int n){
	unsigned long long fact = 1;	//0!= 1, 1!= 1
	for(int i = 2; i <= n ; i++){
		fact *= i;
	}
	return fact;
}
int main(){
	int k = 3;
	int n = 4;
	auto ans = (factorial(n - 1)/factorial(k - 1)) / factorial(n-k);
	cout << ans; //3
	return 0;
}

Code explanation

  • Line 5: The function returns unsigned long long, that is, the maximum integer value it can hold is 9 * 1018. This is less than 21! (= 5 * 1019) and greater than 20!, so we can calculate all values where n < 21.
  • Line 8: Infact *= i , the variable fact initially was (i-1)!. After multiplication with i, fact becomes i!.
  • Lines 14 and 15 : It defines paramters n and k for equation x1 + x2 + ... + xk = n.
  • Line 16: We calculate the binomial coefficient (n−1k−1)=(n−1)!(k−1)!(n−k)! \binom{n-1}{k-1} = \frac{(n-1)!}{ (k-1)!( n-k)!}. bina / (b * c) is calculated as (a / b) / c to prevent overflow where     a=(n−1)!,b=(k−1)!andc=(n−k)!.a = (n -1) ! \hspace{0.15cm}, \hspace{0.15cm} b = (k -1)! \hspace{0.15cm}and \hspace{0.20cm}c = (n - k)!\hspace{0.15cm}.

Time complexity

The time complexity of the above problem is O(n)O(n) which is the time taken to calculate n!n!.

Free Resources

Attributions:
  1. undefined by undefined
License: Creative Commons-Attribution NonCommercial-ShareAlike 4.0 (CC-BY-NC-SA 4.0)