How to check if a binary tree is a binary search tree

A Binary Search Tree (BST) is a binary tree with the following properties:

The left subtree of a particular node will always contain nodes whose keys are less than that node’s key.
The right subtree of a particular node will always contain nodes with keys greater than that node’s key.
The left and right subtree of a particular node will also, in turn, be binary search trees.

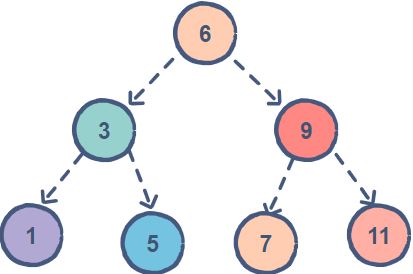
The tree on the right is a BST.

// Including dependancies.
#include <iostream>
#include <limits>
using namespace std;
// A node of a tree.
struct Tree
{
	int data;
	Tree *left;
	Tree *right;
  Tree(int data) 
    { 
        this -> data = data; 
        left = NULL;
        right = NULL; 
    }     
};
// Function to check if a binary tree is a BST. Note that this
// code allows for duplicate keys.
bool isBST(Tree* node, int min, int max) {
	// Base case. An empty tree is a BST.
	if (node == NULL)
		return true;
	// Checking if a key is outside the permitted range.
	if (node -> data <= min)
		return false;
  if (node -> data >= max)
		return false;
	// Sending in updates ranges to the right and left subtree
	return isBST(node -> right, node -> data, max) && 
  isBST(node -> left, min, node -> data);			
}
int main() {
  // Creating a BST
  Tree *root = new Tree(6); 
  root -> left = new Tree(3); 
  root -> right = new Tree(9); 
  root -> left -> left = new Tree(1); 
  root -> left -> right = new Tree(5);
  root -> right -> left = new Tree(7);
  root -> right -> right = new Tree(11);
  // Passing in the min and the max value that can be
  // represented inside an integer.
  int min = std::numeric_limits<int>::min();
  int max = std::numeric_limits<int>::max();
  if(isBST(root, min, max)){
    cout<<"This binary tree is a BST."<<endl;
  }
  else{
    cout<<"This binary tree is not a BST."<<endl;
  }
  return 0;
}

How to check if a binary tree is a binary search tree

Algorithm

Code